IECE - Institute of Emerging and Computer Engineers

  • Sign Up Log in
    Log in

    • -
    CiteScore
    -
    Impact Factor
    1. Home
    2. Journals
    3. IECE Transactions on Emerging Trends in Network Systems
    4. Volume 1, Issue 1
    Volume 1, Issue 1, IECE Transactions on Emerging Trends in Network Systems
    Volume 1, Issue 1, 2024
    Submit Manuscript Edit a Special Issue
    Academic Editor
    Abdur Rasool
    Abdur Rasool
    University of Hawaii at Manoa, Honolulu, USA
    Article QR Code
    Article QR Code
    Scan the QR code for reading
    Popular articles
    Research on A Ship Trajectory Classification Method Based on Deep Learning YOLOv7-Bw: A Dense Small Object Efficient Detector Based on Remote Sensing Image Deep Prediction Network Based on Covariance Intersection Fusion for Sensor Data A Mimic Fusion Algorithm for Dual Channel Video Based on Possibility Distribution Synthesis Theory Visual Feature Extraction and Tracking Method Based on Corner Flow Detection Bridging Modalities: A Survey of Cross-Modal Image-Text Retrieval Inaugural Editorial of the Chinese Journal of Information Fusion Simultaneous Spatiotemporal Bias Compensation and Data Fusion for Asynchronous Multisensor Systems YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems Extraction of Motion Information from Occupancy Grid Map Using Keystone Transform
    IECE Transactions on Emerging Trends in Network Systems, 2024, Volume 1, Issue 1: 5-18

    Free Access | Research Article | 26 December 2024
    Adaptive Fuzzy Controller for Chaos Suppression in Nonlinear Fractional Order Systems
    by
    IECE Author Amin Sharafian 1
    IECE Author Islam Md Monirul 1
    IECE Author Mohammad Jafar Mokarram 1
    IECE Author Inam Ullah 2 *
    1 College of Mechatronics and Control Engineering, Shenzhen University, Shenzhen, China
    2 Department of Computer Engineering, Gachon University, Seongnam 13120, Republic of Korea
    * Corresponding Author: Inam Ullah, [email protected]
    DOI: 10.62762/TETNS.2024.318686
    Received: 30 October 2024, Accepted: 17 December 2024, Published: 26 December 2024  
    Abstract
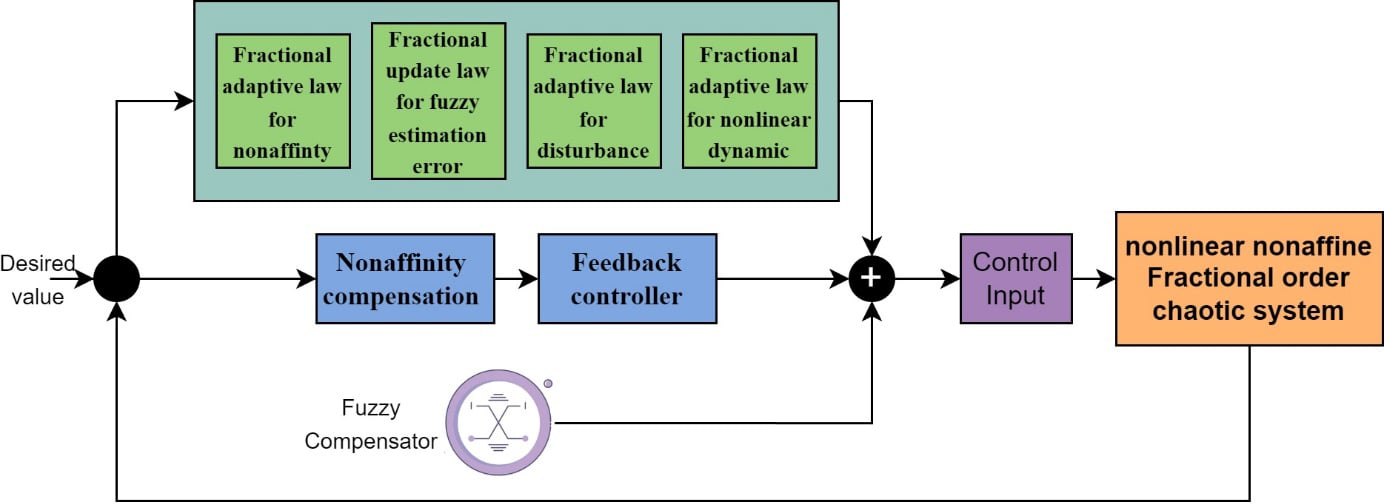
    This paper introduces a novel method for controlling a class of nonlinear non-affine systems with fractional-order dynamics, using an adaptive fuzzy technique. By incorporating a novel fractional update law in the design procedure, the controller can effectively suppress chaotic behaviour and smoothly track desired trajectories. The proposed method offers key advantages such as robustness against uncertainties, fast error convergence to the neighbourhood of zero, and satisfactory disturbance rejection performance. To demonstrate the capabilities of the proposed fractional controller, simulation results were conducted using Python on a fractional order Arneodo chaotic system. The results highlight the effectiveness and potential of the proposed method in controlling fractional-order systems.
    Graphical Abstract
    Adaptive Fuzzy Controller for Chaos Suppression in Nonlinear Fractional Order Systems
    Keywords
    fuzzy
    adaptive
    fractional
    chaos
    arneodo
    Funding
    This work was supported without any funding.
    Cite This Article
    APA Style
    Sharafian, A., Monirul, I. M., Mokarram, M. J., & Ullah, I. (2024). Adaptive Fuzzy Controller for Chaos Suppression in Nonlinear Fractional Order Systems. IECE Transactions on Emerging Trends in Network Systems, 1(1), 5–18. https://doi.org/10.62762/TETNS.2024.318686
    References
    1. Wang, Y. L., Jahanshahi, H., Bekiros, S., Bezzina, F., Chu, Y. M., & Aly, A. A. (2021). Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos, Solitons & Fractals, 146, 110881.
      [Google Scholar]
    2. Baleanu, D., Hasanabadi, M., Vaziri, A. M., & Jajarmi, A. (2023). A new intervention strategy for an HIV/AIDS transmission by a general fractional modeling and an optimal control approach. Chaos, Solitons & Fractals, 167, 113078.
      [Google Scholar]
    3. Monirul, I. M., Qiu, L., & Ruby, R. (2024). Accurate SOC estimation of ternary lithium-ion batteries by HPPC test-based extended Kalman filter. Journal of Energy Storage, 92, 112304.
      [Google Scholar]
    4. Monirul, I. M., Qiu, L., Ruby, R., & Yu, J. (2023). Adaptive state of charge estimation for lithium-ion batteries using feedback-based extended Kalman filter. IET Control Theory & Applications, 17(16), 2162-2177.
      [Google Scholar]
    5. Monirul, I. M., Qiu, L., & Ali, A. (2024, May). Enhanced Unscented Kalman Filter for Accurate State of Charge Estimation in Aerial Drone Lithium-Ion Batteries. In 2024 IEEE 7th International Conference on Industrial Cyber-Physical Systems (ICPS) (pp. 1-6). IEEE.
      [Google Scholar]
    6. Wang, Y., & Zhao, G. (2023). A comparative study of fractional-order models for lithium-ion batteries using Runge Kutta optimizer and electrochemical impedance spectroscopy. Control Engineering Practice, 133, 105451.
      [Google Scholar]
    7. Benbouhenni, H., Bizon, N., Mosaad, M. I., Colak, I., Djilali, A. B., & Gasmi, H. (2024). Enhancement of the power quality of DFIG-based dual-rotor wind turbine systems using fractional order fuzzy controller. Expert Systems with Applications, 238, 121695.
      [Google Scholar]
    8. Sharafian, A., & Ghasemi, R. (2019). Fractional neural observer design for a class of nonlinear fractional chaotic systems. Neural Computing and Applications, 31, 1201-1213.
      [Google Scholar]
    9. Pham, V. T., Kingni, S. T., Volos, C., Jafari, S., & Kapitaniak, T. (2017). A simple three-dimensional fractional-order chaotic system without equilibrium: Dynamics, circuitry implementation, chaos control and synchronization. AEU-international Journal of Electronics and Communications, 78, 220-227.
      [Google Scholar]
    10. Hajipour, A., Hajipour, M., & Baleanu, D. (2018). On the adaptive sliding mode controller for a hyperchaotic fractional-order financial system. Physica A: Statistical Mechanics and its Applications, 497, 139-153.
      [Google Scholar]
    11. Khanzadeh, A., & Pourgholi, M. (2016). Robust synchronization of fractional-order chaotic systems at a pre-specified time using sliding mode controller with time-varying switching surfaces. Chaos, Solitons & Fractals, 91, 69-77.
      [Google Scholar]
    12. Pashaei, S., & Badamchizadeh, M. (2016). A new fractional-order sliding mode controller via a nonlinear disturbance observer for a class of dynamical systems with mismatched disturbances. ISA transactions, 63, 39-48.
      [Google Scholar]
    13. Qiu, L., Yu, J., Monirul, I. M., Liu, C., & Wu, Z. (2023). Consensus control of semi-Markov jump topology multiple direct-drive motion system. IET Control Theory & Applications, 17(15), 2071-2084.
      [Google Scholar]
    14. Aghababa, M. P. (2013). Design of a chatter-free terminal sliding mode controller for nonlinear fractional-order dynamical systems. International Journal of Control, 86(10), 1744-1756.
      [Google Scholar]
    15. Wang, X. Y., & Song, J. M. (2009). Synchronization of the fractional order hyperchaos Lorenz systems with activation feedback control. Communications in Nonlinear Science and Numerical Simulation, 14(8), 3351-3357.
      [Google Scholar]
    16. Qiu, L., Wen, Y., Monirul, I. M., Najariyan, M., Pan, J., & Wu, Z. (2023). Networked $ H_\infty $ Control and Its Applications for a Multi-Station Cooperative Motion System. IEEE Transactions on Automation Science and Engineering, 21(4), 7107-7116.
      [Google Scholar]
    17. Navabi, M., Hashkavaei, N. S., & Reyhanoglu, M. (2023). Satellite attitude control using optimal adaptive and fuzzy controllers. Acta Astronautica, 204, 434-442.
      [Google Scholar]
    18. Lin, Y. H., Yu, C. M., Wu, I. C., & Wu, C. Y. (2023). The depth-keeping performance of autonomous underwater vehicle advancing in waves integrating the diving control system with the adaptive fuzzy controller. Ocean Engineering, 268, 113609.
      [Google Scholar]
    19. Ali, M., Kaur, K., Adnan, M., & Nisar, S. (2023). Adaptive fuzzy controller based early detection and prevention of asymmetrical faults in power systems. Control Engineering Practice, 130, 105380.
      [Google Scholar]
    20. Zangeneh, M., Aghajari, E., & Forouzanfar, M. (2022). A review on optimization of fuzzy controller parameters in robotic applications. IETE Journal of Research, 68(6), 4150-4159.
      [Google Scholar]
    21. Mendoza, A. M. E. R., & Yu, W. (2023). Fuzzy adaptive control law for trajectory tracking based on a fuzzy adaptive neural PID controller of a multi-rotor unmanned aerial vehicle. International Journal of Control, Automation and Systems, 21(2), 658-670.
      [Google Scholar]
    22. He, S., Xu, X., Xie, J., Wang, F., & Liu, Z. (2023). Adaptive control of dual-motor autonomous steering system for intelligent vehicles via Bi-LSTM and fuzzy methods. Control engineering practice, 130, 105362.
      [Google Scholar]
    23. Wei, J., Liu, Y. J., Chen, H., & Liu, L. (2023). Fuzzy adaptive control for vehicular platoons with constraints and unknown dead-zone input. IEEE Transactions on Intelligent Transportation Systems, 24(4), 4403-4412.
      [Google Scholar]
    24. Shen, Q., Shi, P., & Lim, C. P. (2024). Fuzzy adaptive fault-tolerant stability control against novel actuator faults and its application to mechanical systems. IEEE Transactions on Fuzzy Systems, 32(4), 2331-2340.
      [Google Scholar]
    25. Ha, S., Chen, L., Liu, H., & Zhang, S. (2022). Command filtered adaptive fuzzy control of fractional-order nonlinear systems. European Journal of Control, 63, 48-60.
      [Google Scholar]
    26. You, X., Shi, M., Guo, B., Zhu, Y., Lai, W., Dian, S., & Liu, K. (2022). Event-triggered adaptive fuzzy tracking control for a class of fractional-order uncertain nonlinear systems with external disturbance. Chaos, Solitons & Fractals, 161, 112393.
      [Google Scholar]
    27. Yang, W., Zheng, W. X., & Yu, W. (2022). Observer-based event-triggered adaptive fuzzy control for fractional-order time-varying delayed MIMO systems against actuator faults. IEEE Transactions on Fuzzy Systems, 30(12), 5445-5459.
      [Google Scholar]
    28. Shi, J., Cao, J., Liu, H., & Zhang, X. (2023). Compound adaptive fuzzy output feedback control for uncertain fractional-order nonlinear systems with fuzzy dead-zone input. International Journal of Fuzzy Systems, 25(6), 2439-2452.
      [Google Scholar]
    29. Sharifi, A., Sharafian, A., & Ai, Q. (2021). Adaptive MLP neural network controller for consensus tracking of Multi-Agent systems with application to synchronous generators. Expert Systems with Applications, 184, 115460.
      [Google Scholar]
    30. Zhang, X., Zhang, W., Cao, J., & Liu, H. (2024). Observer-based command filtered adaptive fuzzy control for fractional-order MIMO nonlinear systems with unknown dead zones. Expert Systems with Applications, 124623.
      [Google Scholar]
    31. Betalo, M. L., Leng, S., Abishu, H. N., Dharejo, F. A., Seid, A. M., Erbad, A., ... & Guizani, M. (2023). Multi-agent deep reinforcement learning-based task scheduling and resource sharing for O-RAN-empowered multi-UAV-assisted wireless sensor networks. IEEE Transactions on Vehicular Technology, 73(7), 9247-9261.
      [Google Scholar]
    32. Betalo, M. L., Leng, S., Abishu, H. N., Seid, A. M., Fakirah, M., Erbad, A., & Guizani, M. (2024). Multi-agent drl-based energy harvesting for freshness of data in uav-assisted wireless sensor networks. IEEE Transactions on Network and Service Management, 21(6), 6527-6541.
      [Google Scholar]
    33. Sharifi, A., Sharafian, A., & Ai, Q. (2024). Observer-based control for consensus tracking of non-linear synchronous generators system using sliding mode method and a radial basis function neural network. The European Physical Journal Special Topics, 1-22.
      [Google Scholar]
    34. Wang, Q., Pan, Y., Cao, J., & Liu, H. (2023). Adaptive fuzzy echo state network control of fractional-order large-scale nonlinear systems with time-varying deferred constraints. IEEE Transactions on Fuzzy Systems, 32(2), 634-648.
      [Google Scholar]
    35. Ullah, I., Ali, F., Sharafian, A., Ali, A., Naeem, H. Y., & Bai, X. (2024). Optimizing underwater connectivity through multi-attribute decision-making for underwater IoT deployments using remote sensing technologies. Frontiers in Marine Science, 11, 1468481.
      [Google Scholar]
    36. Zou, W., Mao, J., & Xiang, Z. (2024). Adaptive Fuzzy Finite-Time Sampled-Data Control for A Class of Fractional-Order Nonlinear Systems. IEEE Transactions on Fuzzy Systems, 32(5), 3012-3025.
      [Google Scholar]
    37. Luchko, Y., & Yamamoto, M. (2020). The general fractional derivative and related fractional differential equations. Mathematics, 8(12), 2115.
      [Google Scholar]
    38. Sharafian, A., Sharifi, A., & Zhang, W. (2020). Different types of sliding mode controller for nonlinear fractional multi-Agent system. Chaos, Solitons & Fractals, 131, 109481.
      [Google Scholar]
    39. Ha, S., Chen, L., Liu, D., & Liu, H. (2024). Command Filtered Adaptive Fuzzy Control of Fractional-Order Nonlinear Systems With Unknown Dead Zones. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 54(6), 3705-3716.
      [Google Scholar]
    40. Sharafian, A., Ullah, I., Singh, S. K., Ali, A., Khan, H., & Bai, X. (2024). Adaptive fuzzy backstepping secure control for incommensurate fractional order cyber–physical power systems under intermittent denial of service attacks. Chaos, Solitons & Fractals, 186, 115288.
      [Google Scholar]
    41. Qiu, H., Liu, H., & Zhang, X. (2023). Composite adaptive fuzzy backstepping control of uncertain fractional-order nonlinear systems with quantized input. International Journal of Machine Learning and Cybernetics, 14(3), 833-847.
      [Google Scholar]
    42. Sharafian, A., Ali, A., Ullah, I., Khalifa, T. R., Bai, X., & Qiu, L. (2025). Fuzzy adaptive control for consensus tracking in multiagent systems with incommensurate fractional-order dynamics: Application to power systems. Information Sciences, 689, 121455.
      [Google Scholar]
    43. Ullah, I., Adhikari, D., Khan, H., Anwar, M. S., Ahmad, S., & Bai, X. (2024). Mobile robot localization: Current challenges and future prospective. Computer Science Review, 53, 100651.
      [Google Scholar]
    44. Sharafian, A., Kanesan, J., Khairuddin, A. S. M., Ramanathan, A., Sharifi, A., & Bai, X. (2023). A novel approach to state estimation of HIV infection dynamics using fixed-time fractional order observer. Chaos, Solitons & Fractals, 177, 114192.
      [Google Scholar]
    45. Taheri, M., Chen, Y., Zhang, C., Berardehi, Z. R., Roohi, M., & Khooban, M. H. (2023). A finite-time sliding mode control technique for synchronization chaotic fractional-order laser systems with application on encryption of color images. Optik, 285, 170948.
      [Google Scholar]
    46. Zhan, Y., Sui, S., & Tong, S. (2021). Adaptive fuzzy decentralized dynamic surface control for fractional-order nonlinear large-scale systems. IEEE Transactions on Fuzzy Systems, 30(8), 3373-3383.
      [Google Scholar]
    47. Ullah, I., Adhikari, D., Ali, F., Ali, A., Khan, H., Sharafian, A., ... & Bai, X. (2024). Revolutionizing E-Commerce With Consumer-Driven Energy-Efficient WSNs: A Multi-Characteristics Approach. IEEE Transactions on Consumer Electronics.
      [Google Scholar]
    48. Ghasemi, R., Sedighi, M., Ghasemi, M., & Sadat Ghazanfarpoor, B. (2023). Design of a Fuzzy Adaptive Voltage Controller for a Nonlinear Polymer Electrolyte Membrane Fuel Cell with an Unknown Dynamical System. Sustainability, 15(18), 13609.
      [Google Scholar]
    49. Lin, F., Xue, G., Qin, B., Li, S., & Liu, H. (2023). Event-triggered finite-time fuzzy control approach for fractional-order nonlinear chaotic systems with input delay. Chaos, Solitons & Fractals, 175, 114036.
      [Google Scholar]
    50. Ali, S. H., Ullah, I., Ali, S. A., Haq, M. I. U., & Ullah, N. (2024). A Cyber-Physical System Based on On-Board Diagnosis (OBD-II) for Smart City. IECE Transactions on Intelligent Systematics, 1(2), 49-57.
      [Google Scholar]
    51. Li, H., Wang, S., Islam, M., Bobobee, E. D., Zou, C., & Fernandez, C. (2022). A novel state of charge estimation method of lithium-ion batteries based on the IWOA-AdaBoost-Elman algorithm. International journal of energy research, 46(4), 5134-5151.
      [Google Scholar]
    52. Kotaridis, I., & Lazaridou, M. (2021). Remote sensing image segmentation advances: A meta-analysis. ISPRS Journal of Photogrammetry and Remote Sensing, 173, 309-322.
      [Google Scholar]
    Article Metrics
    Citations:

    Google Scholar
    0

    Crossref

    0

    Scopus

    0

    Web of Science

    0
    Article Access Statistics:
    Views: 159
    PDF Downloads: 8
    Publisher's Note
    IECE stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
    Rights and permissions
    IECE or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
    IECE Transactions on Emerging Trends in Network Systems

    IECE Transactions on Emerging Trends in Network Systems

    ISSN: request pending (Online) | ISSN: request pending (Print)

    Email: [email protected]

    Portico

    Portico

    All published articles are preserved here permanently:
    https://www.portico.org/publishers/iece/

    Copyright © 2024 Institute of Emerging and Computer Engineers Inc.