Sustainable Intelligent Infrastructure
ISSN: request pending (Online) | ISSN: request pending (Print)
Email: [email protected]


Earthquakes can trigger a variety of environmental geohazards, presenting significant challenges to both human populations and ecosystems [1]. Some of the environmental geohazards associated with earthquakes have been researched and explored in previous projects. Ground shaking during earthquakes can destabilize slopes, leading to landslides. The rapid movement of soil and rock downhill can pose significant hazards to communities, infrastructure, and transportation routes. In areas with water-saturated, loose soils, the intense shaking from earthquakes can cause the ground to lose strength and behave like a liquid [2]. This phenomenon, known as liquefaction, can result in the sinking, tilting, or lateral spreading of structures and infrastructure. Underwater earthquakes, particularly those occurring along subduction zones, can trigger tsunamis [3]. These massive sea waves can cause devastating impacts on coastal areas, leading to widespread flooding and destruction. Seismic activity along fault lines can cause visible displacement of the ground surface, resulting in ground rupture [3]. This can disrupt infrastructure, alter landscapes, and pose hazards to human safety. Intense ground shaking can lead to increased soil erosion, particularly in hilly or mountainous regions. This erosion can have long-term impacts on ecosystems and agricultural land [4]. Earthquakes can alter the flow of groundwater, leading to changes in aquifer systems, the emergence of new springs, or the disruption of existing water sources [5]. Earthquakes can cause the displacement of natural features such as river courses, lakes, and wetlands, leading to changes in local ecosystems and potential hazards to human settlements [5]. Understanding and mitigating these environmental geohazards is crucial for both disaster preparedness and post-earthquake recovery efforts. This involves comprehensive hazard mapping, land use planning, infrastructure design, and the implementation of early warning systems. This helps mitigate the impacts of earthquakes on the environment and human populations [6]. However, ground movements are associated with earthquake events.
Ground movement encompasses various phenomena related to the Earth’s surface dynamics. Seismic activity refers to the displacement of the Earth’s surface caused by events such as earthquakes or volcanic eruptions [5]. These movements significantly impact the landscape and pose threats to human life and property. Also, soil movement, which is a factor in earthquake studies, can refer to the shifting of soil and sediments due to natural processes like erosion, landslides, or the movement of glaciers [6]. Human activities such as construction, mining, and deforestation can also cause significant soil movement. Tectonic movement is one other factor associated closely to earthquake events and it refers to the movement of the Earth’s tectonic plates, which can cause geological events such as the formation of mountains, rift valleys, and earthquakes [7]. In civil engineering and urban planning, ’ground movement’ refers to the shifting and settling of the ground over time. This phenomenon affects the stability of buildings, roads, and other infrastructure. It can also pertain to the movement of vehicles, pedestrians, and goods within a given area [8]. The specific context determines the precise meaning of ’ground movement’. Under seismic activity, ground movement refers to the shaking, shifting, and deformation of the Earth’s surface. This is caused by the release of energy from within the Earth, typically due to the movement of tectonic plates along faults. This movement can manifest in several ways according to previous studies. These are compressional waves that cause oscillatory motion in the direction of wave propagation [5]. They are the fastest seismic waves and are capable of causing the ground to compress and expand in the direction the wave is traveling. Secondly, these are shear waves that cause vibrations perpendicular to the direction of wave travel. S waves can cause the ground to move up and down or side to side [2]. Surface waves are slower-moving seismic waves that travel along the Earth’s surface, causing the ground to shake in a rolling or swaying motion, similar to ocean waves.The ground movement generated by these seismic waves can have a range of effects. The primary effect of ground shaking is the vibration of buildings, bridges, and other structures, which can lead to structural damage or collapse [1]. In areas with loose, water-saturated soils, seismic waves can cause the ground to behave like a liquid, leading to the loss of soil strength and the sinking or tilting of structures. Seismic activity can trigger landslides by destabilizing slopes, leading to the rapid movement of large amounts of soil and rock [7]. Along active faults, seismic activity can cause the ground to crack and shift, resulting in visible surface ruptures [11]. Seismic waves can cause permanent horizontal or vertical ground displacement, altering the landscape and damaging infrastructure. Understanding and mitigating the effects of ground movement under seismic activity is crucial for designing earthquake-resistant buildings and infrastructure, as well as for developing effective emergency response and recovery plans [10].
Earthquake-induced ground movement, also known as seismic ground motion, refers to the oscillatory and translational displacement of the Earth’s surface during an earthquake [2]. This ground movement results from the propagation of seismic waves through the Earth due to the sudden release of energy along faults. Seismic ground motion has several significant effects, as documented in previous studies. Along active faults, the movement caused by an earthquake results in visible ground surface displacement, leading to surface ruptures or fault movements [4]. Following a major earthquake, aftershocks can further contribute to ground movement, causing additional damage to already compromised structures [8]. Understanding earthquake-induced ground movement is essential for assessing seismic hazards and designing earthquake-resistant structures and infrastructure [9]. Engineers and seismologists characterize ground motion using seismic instruments and conduct seismic hazard assessments to inform building codes, land use planning, and emergency preparedness in earthquake-prone regions.
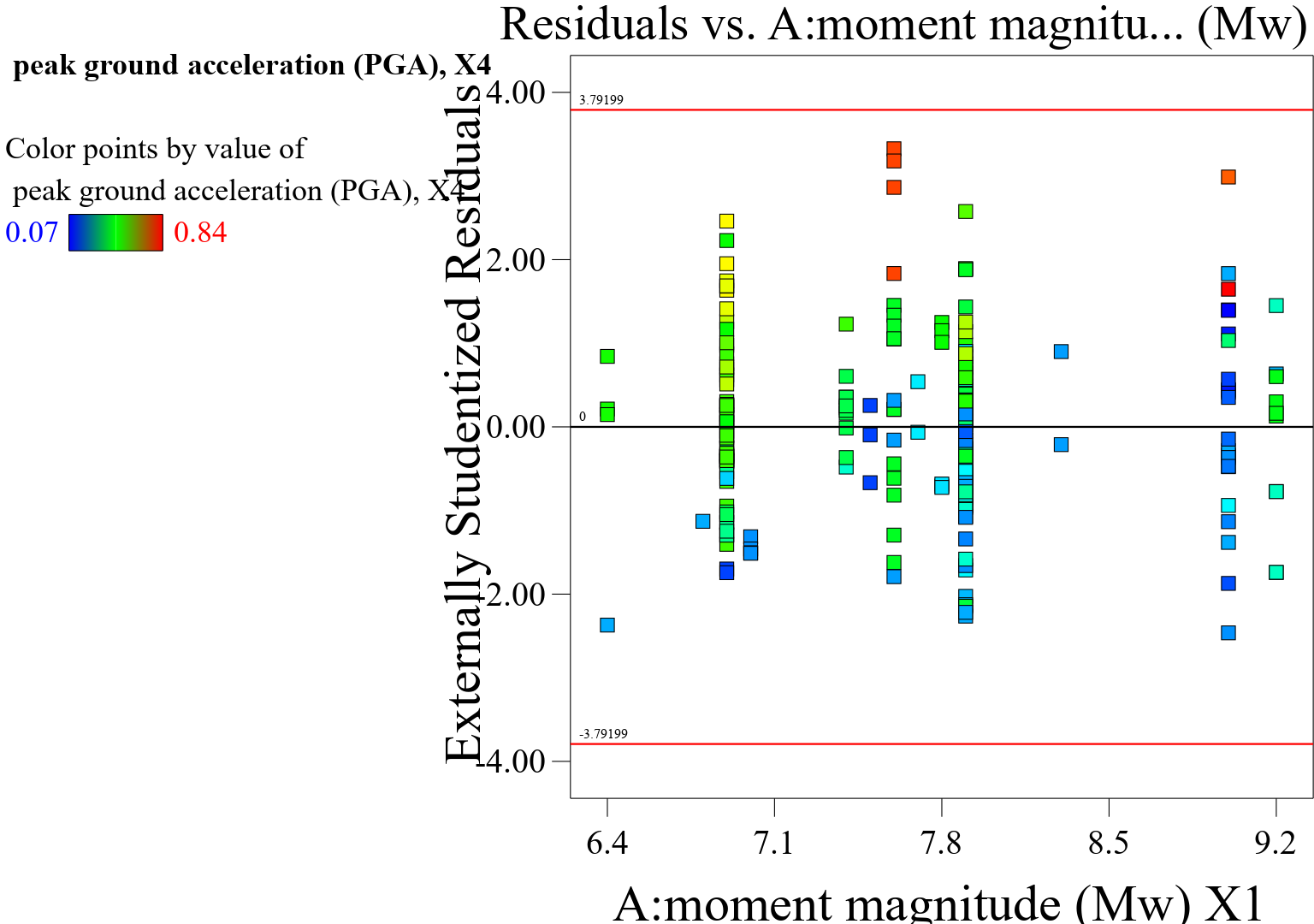
Liu et al. [1] examined three Probabilistic Displacement Models (PDMs) alongside 11 additional models to analyze earthquake-induced landslides (ELHA) in a region impacted by the 1994 Mw 6.7 Northridge earthquake. The findings indicate that PDMs employing pulse-like ground motions (PLGM) require fewer ground motion data, yet exhibit greater precision in landslip prediction. The study utilized the ELHA approach to examine a particular region along the Sichuan-Tibet Railway. The findings indicated that PLGM (Probabilistic Landslide Generation Model) accurately forecasted a higher number of landslide occurrences. This underscores the importance of conducting early investigations and implementing protective measures. Liu et al. [2] introduced four predictive displacement models (PDMs) that take into account pulse-like ground movements (PLGMs) for both strike-slip and non-strike-slip occurrences. The results indicated that PP models exhibit higher accuracy in non-strike-slip events, but their effectiveness may be disregarded in strike-slip events. These findings are relevant for assessing the hazard of earthquake-induced landslides. Another, Dupuis et al. [3] created a machine learning algorithm to assess the accuracy of earthquake ground-motion records in New Zealand. The model, which underwent training using 1096 sample records, successfully reproduced manual quality classifications for three engineering applications. The system is capable of processing records with one, two, or three components, and offers versatility in evaluating record quality according to various criteria. A total of 43,398 ground motions from GeoNet were utilized in the application of the model for the creation of a new curated database. Otárola et al. [4] presented a simulation-based methodology that aims to measure the influence of the length of ground motion caused by earthquakes on the direct economic losses of a portfolio of buildings. The framework encompasses three different building typologies that represent certain vulnerability classes in Southern Italy. These typologies include non-ductile moment-resisting reinforced concrete (RC) infilled frames, as well as ductile moment-resisting RC infilled and bare frames. The analysis involves conducting event-based probabilistic seismic hazard analysis and deriving fragility models for each type of building. The study rigorously evaluated the portfolio loss exceedance curves and predicted yearly losses calculated for each combination of exposure, hazard, and vulnerability models. The influence of the time period on estimations of loss can be substantial, with differences becoming more pronounced as the distance between the defect and the portfolio increases. Also, Armstrong et al. [5] identified the optimal ground motion intensity measures (IMs) for accurately forecasting earthquake loading levels in seismic hazard analysis (SHA). The Arias intensity (AI) model was determined to be the most effective predictor of dam deformations based on the findings of nonlinear deformation analysis (NDA) conducted on two embankment dams. Nevertheless, it was discovered that pseudo-spectral acceleration (PSA)-based intensity measures (IMs) were less efficient. Chen et al. [6] presented a methodology for analyzing earthquake-triggered landslides caused by pulse-like ground motion (PLGM) through the use of discontinuous deformation analysis (DDA). It delineates two perplexing occurrences: extensive landslides in regions with low Peak Ground Acceleration (PGA) and collapsed slopes in regions with high PGA. The paper examines the behavior of a symmetrical slope model in the presence of two earthquakes and concludes that PLGM (Probabilistic Limit Equilibrium Method) has the potential to induce landslides in places close to the fault line during an earthquake. The proposed mechanism examines the tensile and shear strengths of slopes, elucidating the phenomena of landslip initiation during the Kumamoto earthquake in 2016 and the Hokkaido earthquake in 2018. In other studies, Hacıefendioğlu et al. [7] employed a deep learning algorithm to recognize areas of ground failure caused by the earthquake and identify structures that were partially damaged in the Palu earthquake region of Indonesia in 2018. The dataset comprises 392 photos depicting ground failure caused by earthquakes and 223 images showing places that have been affected. The investigation demonstrates that deep learning approaches based on object detection may efficiently identify the consequences of ground collapse caused by earthquakes and recognize damaged structures. Li et al. [8] introduced a spatial division technique and a zoning casualty prediction technique utilizing support vector regression (SVR) for areas affected by earthquakes. The process involves assessing significant factors affecting the number of fatalities in seismic events, dividing the region into zones based on risk levels, and creating a zoning support vector regression model (Z-SVR) with the most effective parameters. The model surpasses existing machine learning techniques and has the ability to improve the accuracy of casualty prediction, which is essential for emergency response and rescue operations. Gitis et al. [9] presented two machine learning techniques for predicting seismic hazards: geographical prediction of the highest potential earthquake magnitudes and spatial-temporal prediction of intense earthquakes. The initial approach employs regression to estimate interval expert assessments, formalize knowledge, and generate spatial forecast maps. The second approach utilizes historical data to pinpoint regions prone to significant seismic activity. The testing conducted in the Mediterranean and Californian regions demonstrated a commendable level of forecast accuracy. Liu et al. [10] developed new machine learning models for subduction earthquake zones by utilizing the NGA-Sub ground motion database. The models rely on various characteristics, including yield coefficient, initial fundamental period, earthquake magnitude, peak ground velocity, and pseudo-spectral acceleration. Five machine learning models are created utilizing contemporary machine learning techniques, which include ridge regression, random forest, gradient boosting decision tree, support vector regression, and residual neural network. These models surpass standard models in terms of predictive accuracy, ability to detect patterns, and efficiency in terms of computer resources required for training. Additionally, they improve the handling of epistemic uncertainty when predicting D, due to the limited availability of reliable models for subduction zone tectonic settings. Noman et al. [11] examined the evaluation of seismic risks in the construction of machine foundations and highlighted important areas for further research. The text explores the various aspects that affect evaluation, the difficulties encountered, and the consequences of dynamic loads and soil-structure interaction. Primary areas of research involve enhancing seismic hazard assessment approaches by numerical modeling techniques and undertaking extensive experimental investigations to validate these models and comprehend the behavior of machine foundations under seismic loads. Other studies, Harirchian et al. [12] employed four Machine Learning (ML) methodologies, namely Support Vector Regression, Stochastic Gradient Descent, Random Forest, and Linear Regression, to generate fragility curves that represent the likelihood of collapse based on Peak Ground Acceleration. The study utilized data collected on-site from 646 masonry walls in Malawi and evaluates the effectiveness and precision of each machine learning approach. The Random Forest (RF) algorithm demonstrates superior efficiency by achieving the lowest values for both the Mean Absolute Percentage Error (MAPE) and Root Mean Square Error (RMSE). This underscores the potential of machine learning techniques in producing precise fragility curves. Bouckovalas et al. [13] used an analytical methodology to forecast the long-term establishment of foundations when they are exposed to seismic vibrations. Centrifuge tests are used to assess the validity. The analyses demonstrated a strong correlation between the predicted and measured responses. Additionally, it is observed that partial drainage can take place during high-frequency dynamic loadings, which has a major impact on settlements and excess pore pressures. Xie et al. [14] examined the advancements and difficulties encountered in the field of machine learning (ML) as applied to earthquake engineering. The specific areas of attention include seismic hazard analysis, system identification, damage detection, fragility evaluation, and structural control. The text provides case stories and addresses research challenges. Machine Learning (ML) is regarded as a potential technology for addressing earthquake engineering difficulties. However, additional research is required to expedite its implementation. Matsagar [15] provided an overview of earthquake engineering and technology, including many specialized areas, current methodologies, and recent advancements. The subject matter encompasses seismology, plate tectonics, and the factors that contribute to earthquakes in the Himalayan subduction zone. The conversation transitions to the field of geotechnical and structural earthquake engineering, specifically focusing on seismic soil-structure interaction (SSI). The discussion focused on infrastructure resilience and the development of a seismic design philosophy through performance-based research. This study discussed advanced devices for modifying dynamic responses, such as damping devices, as well as methods for controlling the structure. Emphasis is placed on future research for students and researchers. Previous studies have modeled this problem applying machine learning such as ensemble techniques, which are only applicable electronically. However, the present research paper has tried to apply a symbolic regression such as the Response Surface Methodology (RSM), which proposes a closed-form equation with which the model can be applied both electronically and manually.
A dataset comprising 234 records was globally compiled from post-earthquake observations, focusing on suspected liquefaction sites characterized by a gravelly soil profile, as documented in prior literature [16]. Each record includes diverse data points, which are the input variables such as the earthquake’s moment magnitude (Mw) represented by , epicenter distance (R) denoted as in kilometers, bracketed duration (t) indicated by in seconds, gravel content (G) as in percentage, fines content (F) denoted by in percentage, average particle size (D50) represented by in millimeters, overburden stress-corrected dynamic penetration test blow count (N’120 Blows) indicated by , vertical effective overburden stress (’v) represented by in kilopascals (kPa), depth to the water table (Dw) as in meters, thickness of the impermeable capping layer (Hn) denoted by in meters, and thickness of the unsaturated zone between the groundwater table and capping layer (Dn) as in meters. The output is the peak ground acceleration (PGA) measured in gravitational units (g) and represented as . The statistical characteristics and the Pearson correlation matrix for the dataset are succinctly conducted and summarized.
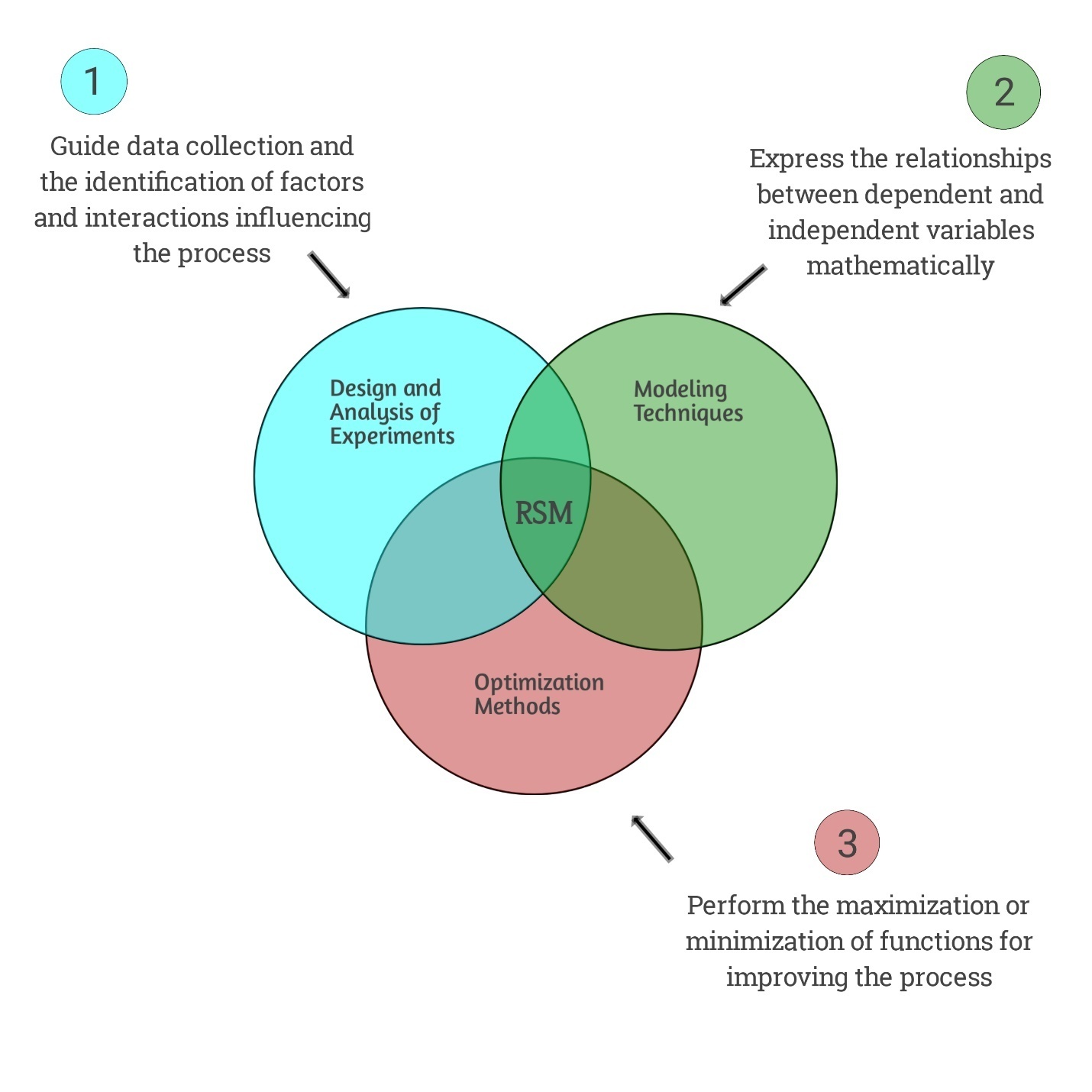
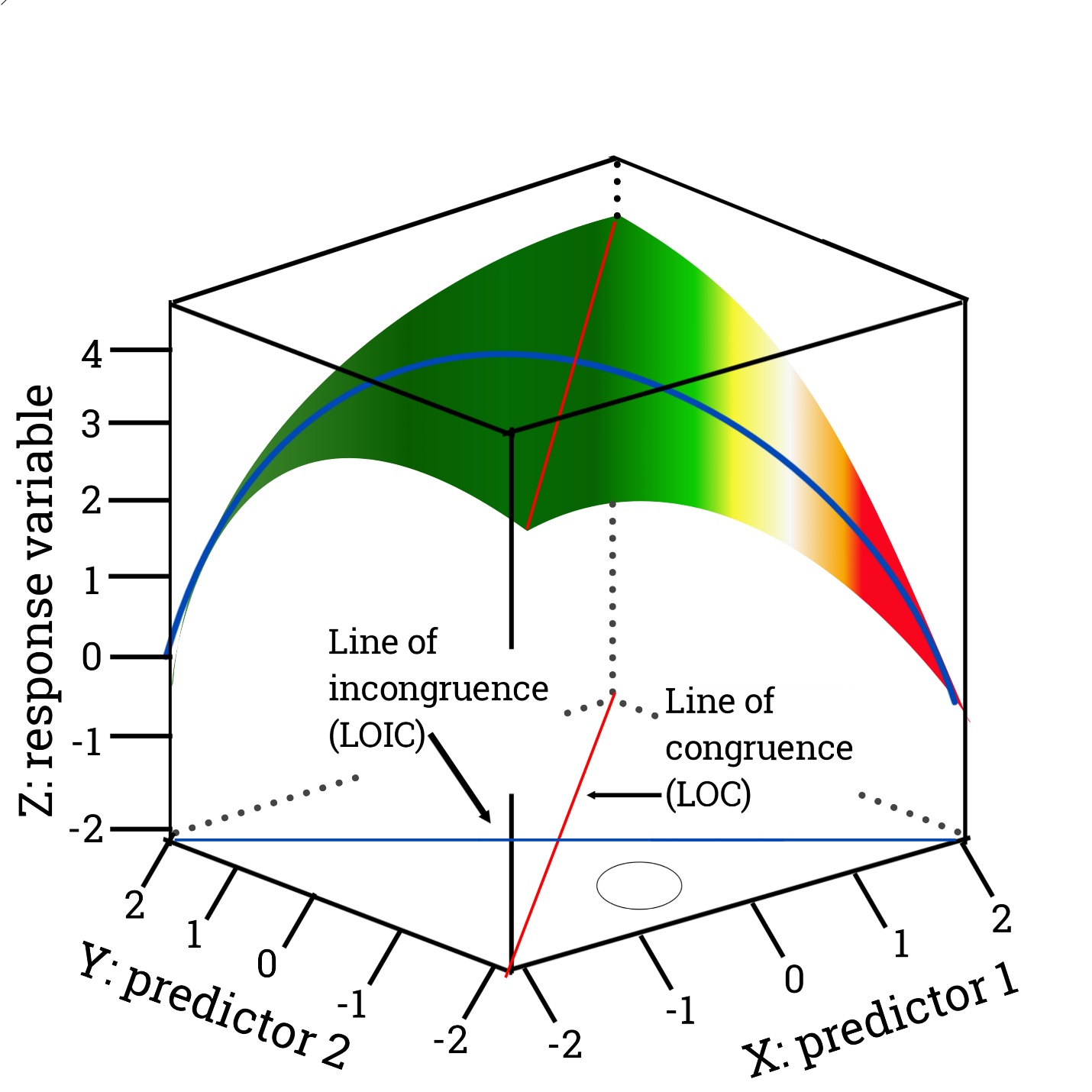
Response Surface Methodology (RSM) is a collection of mathematical and statistical techniques used for modeling and analyzing the relationships between multiple variables and the response of a system [17]. The RSM flow chart of modeling optimization and the 3D surface framework are represented in Figures 1 and 2. It is commonly applied in scientific and engineering fields, particularly in the optimization of complex processes, product development, and quality improvement. RSM is often used to explore and optimize the response of a system within a specific region of the design space. RSM often begins with the design of experiments to systematically collect data on the response of a system as a function of multiple input variables [18]. These experiments are designed to efficiently explore the design space and capture the relationships between inputs and outputs. Using regression analysis and other statistical techniques, mathematical models are developed to represent the relationship between the input variables and the system’s response. These models may include linear, quadratic, and interaction terms to capture the behavior of the system. Once the models are developed, optimization techniques are employed to identify the optimal settings for the input variables that lead to the desired response of the system [19]. This involves finding the input combinations that maximize or minimize the response based on specific criteria. The models developed using RSM are validated to ensure their accuracy and reliability. This may involve conducting additional experiments to confirm the predicted responses based on the optimized input variables. RSM often involves the graphical representation of response surfaces, contour plots, and other visual tools to help understand the relationships between the input variables and the system’s response [20]. Applications of RSM can be found in various fields, including chemical engineering, pharmaceuticals, food science, agriculture, manufacturing, and product development. It is a powerful tool for efficiently optimizing processes and products, reducing experimentation costs, and gaining a deeper understanding of complex systems [18]. Response Surface Methodology (RSM) utilizes mathematical models to characterize and optimize the behavior of complex systems. These models can be classified based on their structure and the nature of the relationships they represent. The linear RSM models describe the relationship between the input variables and the response as a linear function. A simple linear model may include terms for each input variable, while a multiple linear regression model can include interaction terms as well. However, linear models may not always capture the full complexity of a system’s behavior [17]. The Quadratic RSMmodels extend linear models by including squared terms for the input variables. This allows for the representation of nonlinear relationships between variables and the response. Quadratic models are particularly useful for capturing curvature in the response surface. Interaction Models: Interaction models include terms that represent the interaction effects between input variables [20]. These terms capture the combined effect of two or more variables on the response, allowing for the representation of non-additive relationships. The full cubic RSMmodels go beyond quadratic models by including cubic terms for the input variables. These models can capture more complex nonlinear behavior, including inflection points and more pronounced curvatures in the response surface. In addition to the aforementioned models, RSM can incorporate higher-order terms to capture even more complex relationships [19]. This may include models with terms representing higher powers of the input variables, allowing for the representation of highly nonlinear behavior. In cases where the number of input variables is large, fractional factorial designs can be used to construct reduced models that capture the most important effects. These models provide a more efficient way to explore the design space and identify key factors. The selection of the appropriate model type in RSM depends on the nature of the system being studied, the complexity of the relationships, and the available experimental data. Model selection is typically guided by statistical criteria, such as goodness of fit, predictive capability, and the trade-off between model complexity and interpretability [21]. Once a model is selected, it can be used for optimization and prediction within the specified experimental region.
| Std. Dev. | Mean | C.V. % | R² | Adjusted R² | Predicted R² | Adeq Precision |
| 0.117 | 0.3535 | 33.1 | 0.9915 | 0.9846 | 0.9997 | 11.1577 |
In Response Surface Methodology (RSM), the mathematical formulation involves developing equations to model the relationship between the input variables and the response of a system. The most common form of the mathematical equation used in RSM is the response surface model. This can take different forms based on the complexity of the relationships being studied. Here are the general forms of the mathematical equations used in RSM: Linear Model: The general form of a linear model in RSM with two input variables ( and ) can be expressed as [20]:
where, Y represents the response variable, is the intercept, and are the coefficients for the first and second input variables, and , and represents the error term. Quadratic Model: A quadratic model extends the linear model by including squared terms for the input variables, and can be expressed as:
where, and represent the coefficients for the squared terms of and , and represents the coefficient for the interaction term. Interaction Model: An interaction model includes terms that represent the interaction effects between input variables, and can be expressed as:
where represents the coefficient for the interaction term. Cubic Model: A cubic model extends the quadratic model by including cubic terms for the input variables, and can be expressed as:
In this equation, and represent the coefficients for the cubic terms of and . The general response surface model encompasses higher-order terms and can be expressed as a more complex equation that includes linear, quadratic, cubic, and possibly higher-order terms, as well as interaction terms [21]. In the above equations, the coefficients represent the parameters to be estimated from the experimental data, and represents the error term. These equations are derived through regression analysis based on the experimental data collected using designed experiments [22]. The selection of the appropriate model is based on the nature of the relationships between the input variables and the response, and is guided by statistical criteria and the complexity of the system under study. However, the general equation for a response surface model (RSM) can be expressed as:
where Y is the predicted response variable, is the model intercept, , , , etc., are the coefficients for the linear, quadratic, and interaction terms, respectively, , , , etc., are the independent variables (factors) at different levels and is the error term. In this equation, the model can include both linear and nonlinear terms to capture the relationship between the independent variables and the response [21]. The coefficients are estimated through methods such as least squares regression, and the model can be used to analyze and optimize processes in fields such as engineering, chemistry, and manufacturing.
As presented in Table 1, apositive predicted of 0.9997 implies that the overall mean may not be a better predictor of the response than the current model. In some cases, a higher-order model may also predict better. Adequate precision measures the signal-to-noise ratio. A ratio greater than 4 is desirable. This shows the PGA model’s ability to navigate the design space for the design of earthquake-induced ground movement events across the world. Adequate precision and navigation of design space are concepts commonly encountered in the context of experimental design and optimization. Adequate precision refers to the level of accuracy and reliability in the measurements and predictions obtained from a given experimental or predictive model. In the context of experimental design, adequate precision implies that the experimental setup and the associated statistical analysis are capable of providing results that are sufficiently accurate and consistent to draw valid conclusions. For predictive models, adequate precision indicates that the model’s predictions are reliable and provide meaningful insights on the design space navigation. Design space refers to the range of input variables or parameters that can be manipulated within a given system or process. Navigation of design space involves exploring and understanding the relationships between input variables and their effects on the output or response of interest. It often involves the use of techniques such as response surface methodology, design of experiments, optimization algorithms, and sensitivity analysis to systematically explore the design space, identify influential factors, and optimize the system’s performance. In practice, achieving adequate precision and effectively navigating the design space are critical for conducting meaningful experiments, developing accurate predictive models, and optimizing processes or products in various fields such as engineering, manufacturing, and scientific research. These concepts are fundamental to the successful implementation of methodologies aimed at understanding and improving complex systems. The present model’s adequate precision ratio is 11.158, which indicates an adequate signal. This model, however, can be used to navigate the design space.
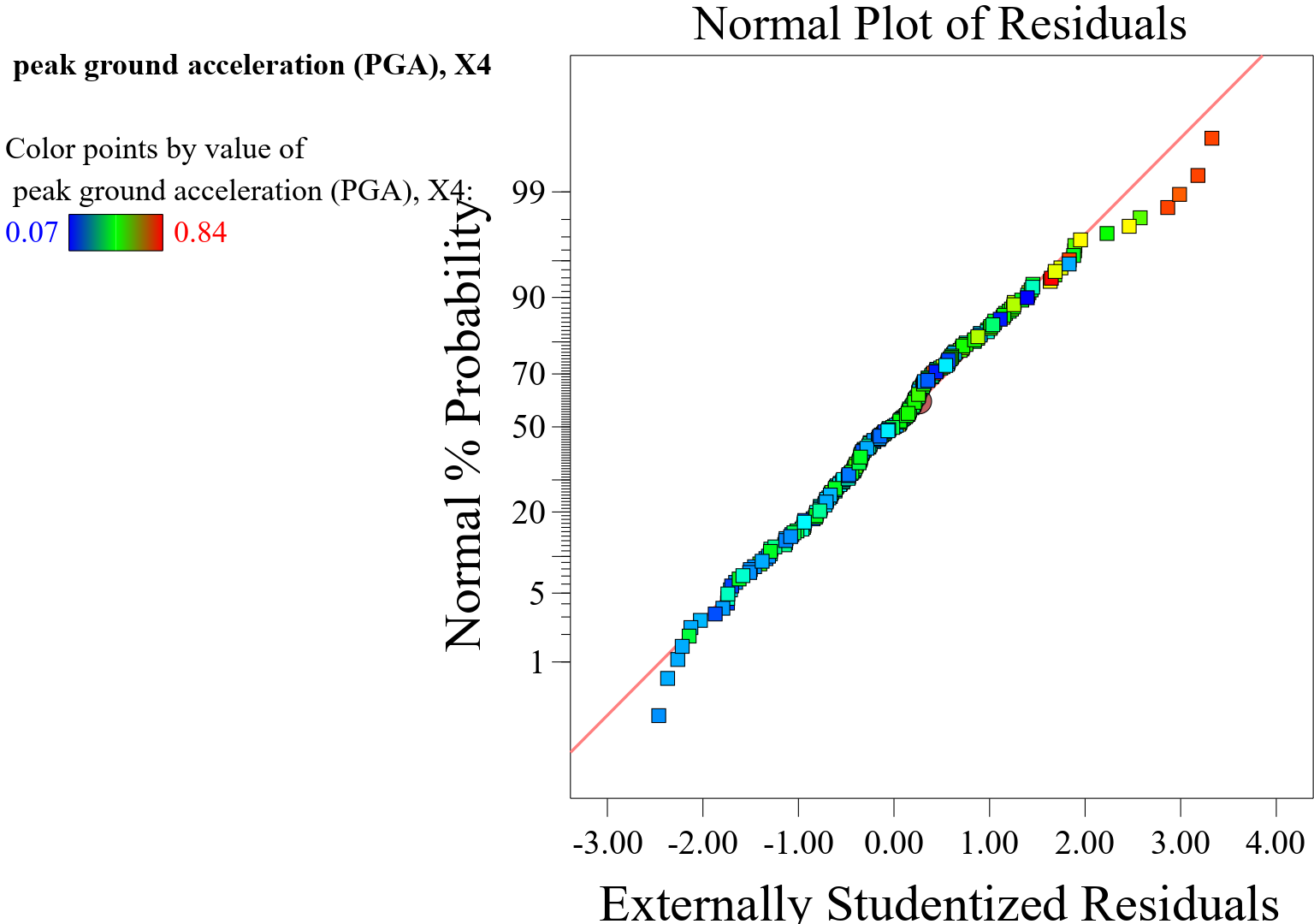
In the context of a response surface model (RSM), a normal plot of residuals presented in Figure 3 is a graphical tool used to assess the assumption of normality for the residuals of the model. The normal plot, also known as a normal probability plot, is a diagnostic tool that helps to determine whether the residuals follow a normal distribution, which is a key assumption for many statistical analyses. Interpreting a normal plot of residuals for an RSM model involves examining how the points on the plot align with the diagonal line, which represents a theoretical normal distribution. If the points on the normal plot approximately form a straight line that closely follows the diagonal line, it suggests that the residuals are approximately normally distributed as shown. This alignment indicates that the normality assumption in the prediction of the PGA is reasonable, supporting the validity of the statistical inferences drawn from the model. But if the points on the normal plot had deviated substantially from the diagonal line, showing a pronounced curvature or systematic departure from linearity, it may indicate non-normality in the residuals. This could imply issues such as skewness, heavy tails, or other departures from the normal distribution. Additionally, the normal plot can reveal information about the presence of outliers or heavy tails in the residuals. Outliers may appear as points that deviate significantly from the expected pattern on the plot, providing insights into potential influential observations. Ultimately, the normal plot of residuals serves as a visual aid for assessing the distributional assumptions of the residuals in an RSM model. Deviations from the expected pattern in the plot can prompt further investigation into the adequacy of the model and potential improvements, such as exploring alternative modeling techniques or identifying influential data points.
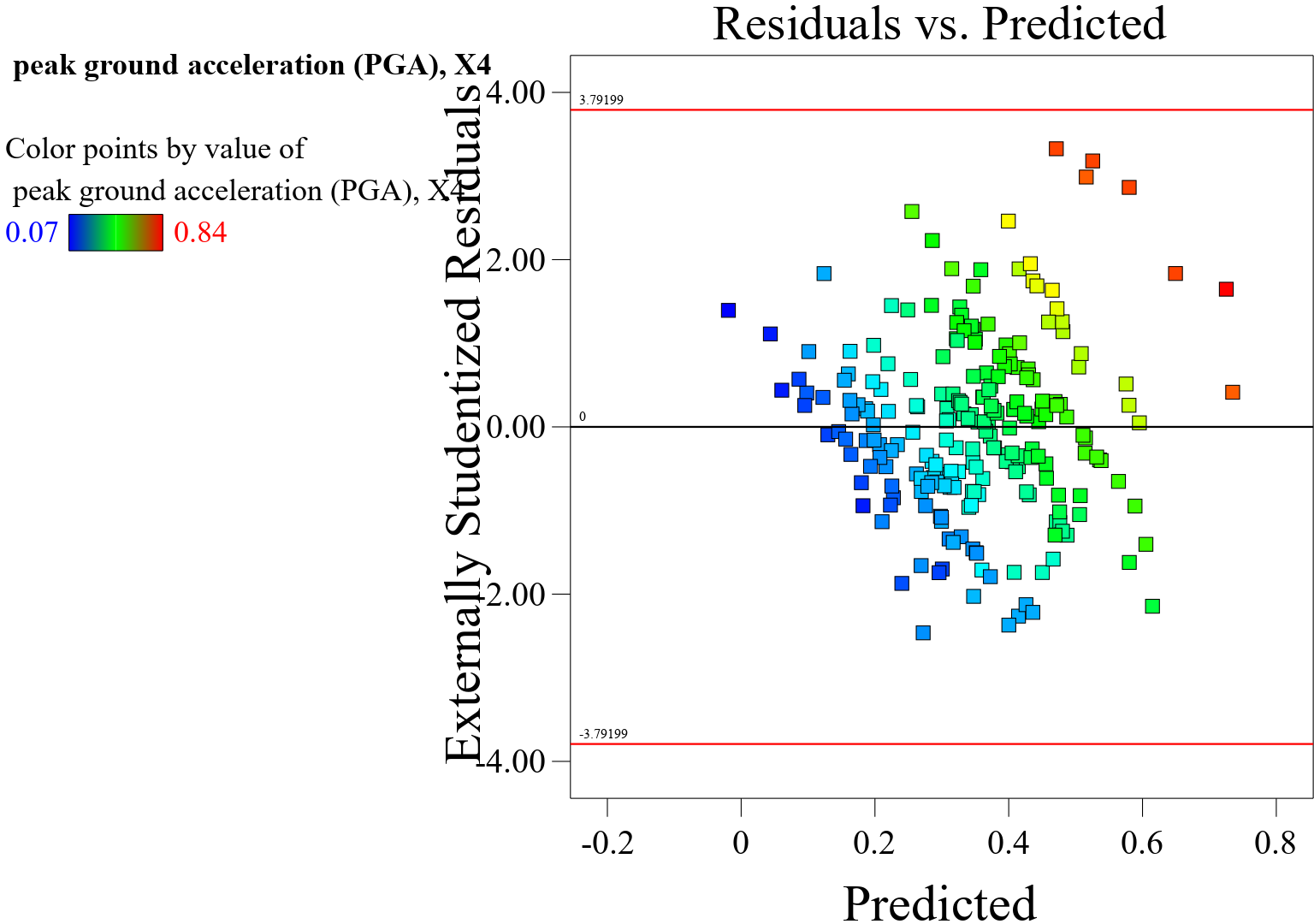
The plot of residuals versus predicted values illustrated in Figure 4 in a response surface model (RSM) is a diagnostic tool used to assess the appropriateness of the model and to detect potential patterns or trends in the residuals. Ideally, the plot should exhibit a random scatter of points around the horizontal line at zero. This indicates that the residuals are not systematically related to the predicted values, suggesting that the model’s assumptions are being met. If the plot shows discernible patterns, such as a systematic increase or decrease in the residuals as the predicted values change, it may indicate potential issues with the model. For example, if the residuals tend to increase or decrease as the predicted values increase, this could suggest that the model is missing important terms or has a non-linear relationship with the response. Patterns in the spread of residuals at different predicted values can also be indicative of heteroscedasticity, where the variability of the residuals changes across the range of predicted values. This can be a concern as it violates the assumption of homoscedasticity, which assumes that the variance of the residuals is constant across the range of predicted values. The plot can also help identify potential outliers or influential data points that have a large impact on the model’s performance. Outliers may appear as points that deviate significantly from the expected random scatter, potentially warranting further investigation. Overall, the plot of residuals versus predicted values serves as a valuable diagnostic tool for assessing the adequacy of the RSM model. It helps in identifying potential model misspecification, non-linearity, heteroscedasticity, and influential observations. In summary, the plot of residuals versus predicted values provides insights into the performance and appropriateness of the RSM model, helping to identify areas where the model may need improvement or where further investigation is warranted.
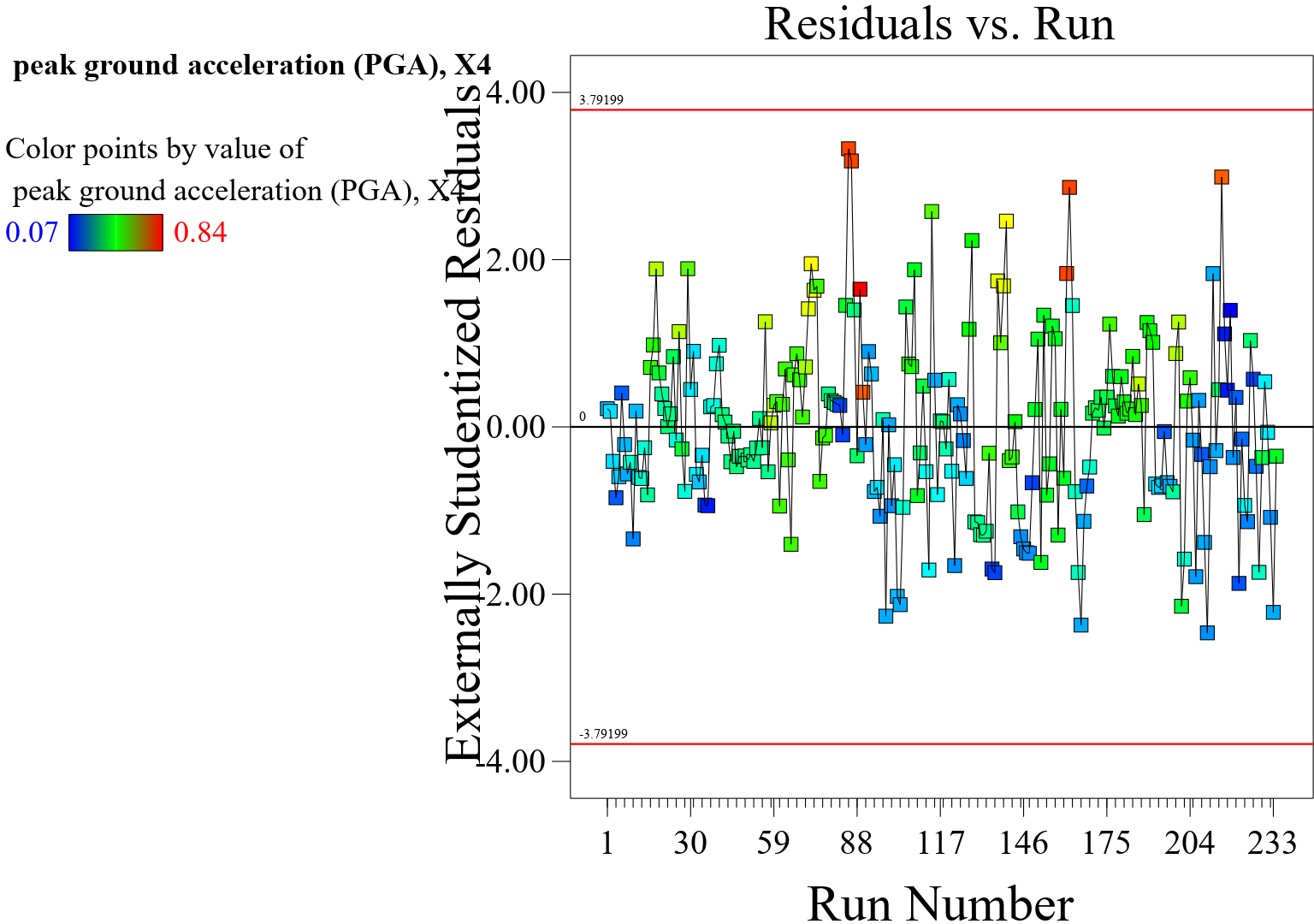
The plot of residuals versus experimental run values presented in Figure 5 in a response surface model (RSM) is a diagnostic tool used to assess the quality and appropriateness of the model. It helps in identifying potential patterns or trends in the residuals with respect to the experimental run values. Ideally, the plot should exhibit a random scatter of points around the horizontal line at zero. This indicates that the residuals are not systematically related to the experimental run values, suggesting that the model’s assumptions are being met. If the plot shows discernible patterns, such as a systematic increase or decrease in the residuals as the experimental run values change, it may indicate potential issues with the model. For example, if the residuals tend to increase or decrease as the experimental run values increase, this could suggest that the model is missing important terms or has a non-linear relationship with the response. Patterns in the spread of residuals at different experimental run values can also be indicative of heteroscedasticity, where the variability of the residuals changes across the range of experimental run values [23]. This can be a concern as it violates the assumption of homoscedasticity, which assumes that the variance of the residuals is constant across the range of experimental run values. The plot can help identify potential outliers or influential data points that have a large impact on the model’s performance. Outliers may appear as points that deviate significantly from the expected random scatter, warranting further investigation. Overall, the plot of residuals versus experimental run values serves as a valuable diagnostic tool for assessing the adequacy of the RSM model. It helps in identifying potential model misspecification, non-linearity, heteroscedasticity, and influential observations. In summary, the plot of residuals versus experimental run values provides insights into the performance and appropriateness of the RSM model, helping to identify areas where the model may need improvement or further investigation.

In the context of a response surface model (RSM), Cook’s distance illustrated in Figure 6 is a measure used to identify influential data points that have a disproportionately large impact on the estimated coefficients of the model. It is a useful diagnostic tool for detecting influential observations, which, if left unaddressed, can significantly affect the model’s fit and predictions. Observations with large Cook’s distances are considered influential, meaning they have a strong influence on the model’s coefficients. In the plot, influential points are typically represented by data points with high Cook’s distances, often plotted above a certain threshold line. Large Cook’s distances indicate that certain observations may substantially affect the model’s fit and predictions. These observations may have a notable impact on the estimated coefficients and can potentially distort the overall model performance. When reviewing the plot of Cook’s distance, researchers can use it as a guide for deciding whether to take corrective actions, such as potentially removing influential observations, transforming variables, or considering alternative modeling approaches to address the impact of these points. Interpretation of Cook’s distance should take into account the specific context of the data and the goals of the analysis. In some cases, influential observations may be an essential part of the dataset, and removing them may not be appropriate without careful consideration of the underlying reasons for their influence. In summary, the plot of Cook’s distance in an RSM model provides valuable insights into influential observations that may have a significant impact on the model’s coefficients and predictive performance. It serves as a diagnostic tool to guide decisions related to model adjustments and the treatment of influential data points.
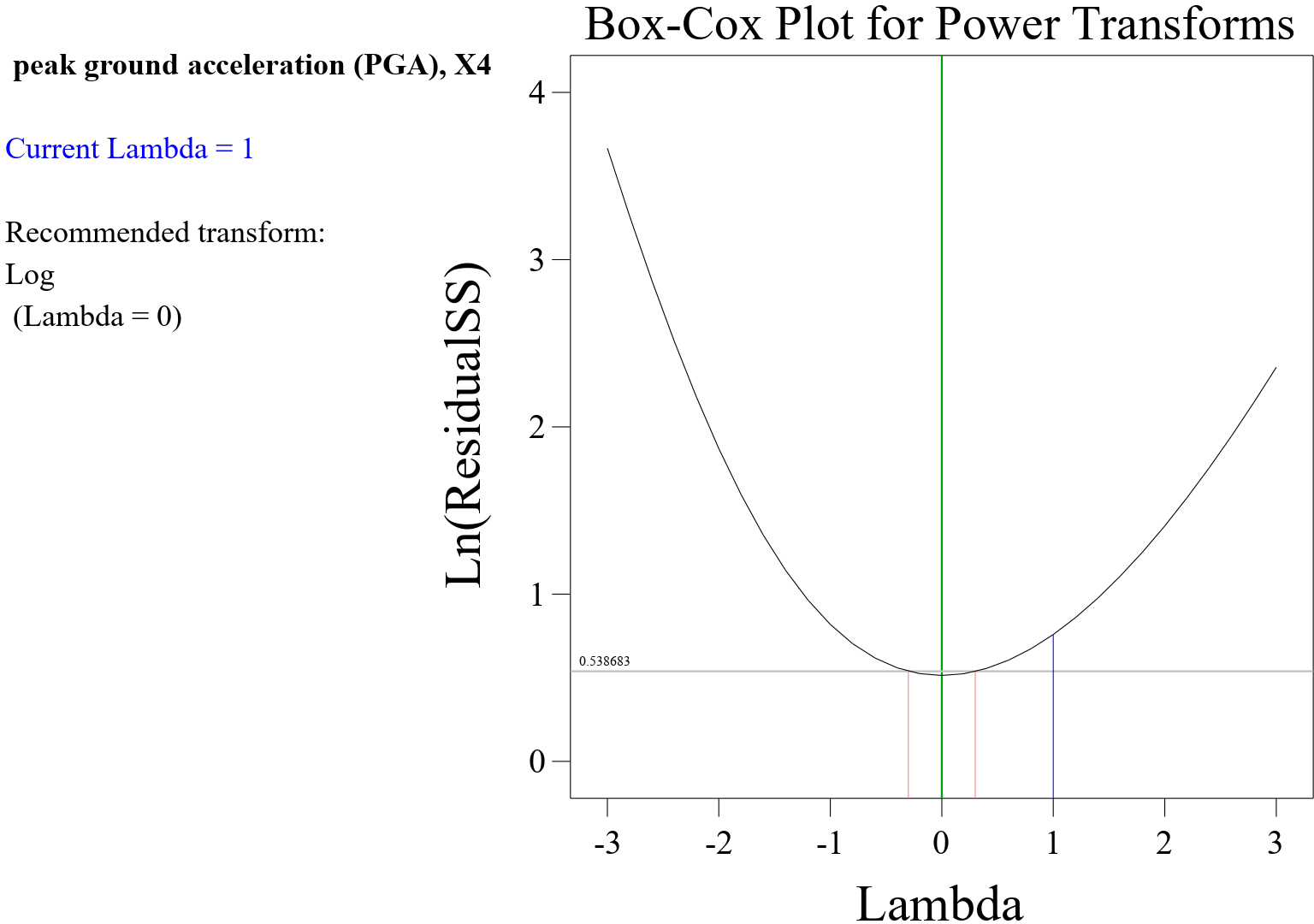
The Box-Cox plot presented in Figure 7 is a diagnostic tool used to identify an appropriate power transformation for the PGA(response variable) in this response surface model (RSM) or any other statistical model. The goal of the Box-Cox transformation is to stabilize the variance and make the data more closely approximate a normal distribution, thus meeting the assumptions of many statistical models. In a Box-Cox plot, the x-axis represents the values of lambda (), which is the power parameter used in the Box-Cox transformation. Lambda values are typically plotted within a range, often from -2 to 2, representing different potential transformations. On the y-axis, the plot typically displays a measure of the transformed data’s normality, such as the log-likelihood function or another suitable metric. This allows you to assess how well the data conforms to normality under different transformation scenarios. The goal of the Box-Cox plot illustrated in Figure 7 is to identify the lambda value that maximizes the normality of the transformed data. This is often indicated by the lambda value that corresponds to the peak or plateau in the plot (see Figure 8), where the transformed data best approximates a normal distribution. When interpreting the Box-Cox plot, you should look for the lambda value that provides the best improvement in normality. A lambda of 0 represents a log transformation, and as the lambda value deviates from 0, it represents different power transformations. The plot helps in visualizing the impact of these transformations on the normality of the data. Once an appropriate lambda value is identified from the Box-Cox plot, the RSM model can be re-estimated using the transformed response variable. This can lead to improved model performance, especially if the original data exhibited issues such as heteroscedasticity or non-normality. In summary, the Box-Cox plot for power transform in an RSM model is used to identify an appropriate power transformation for the response variable, with the aim of improving the normality and variance properties of the data, thus enhancing the model’s performance.
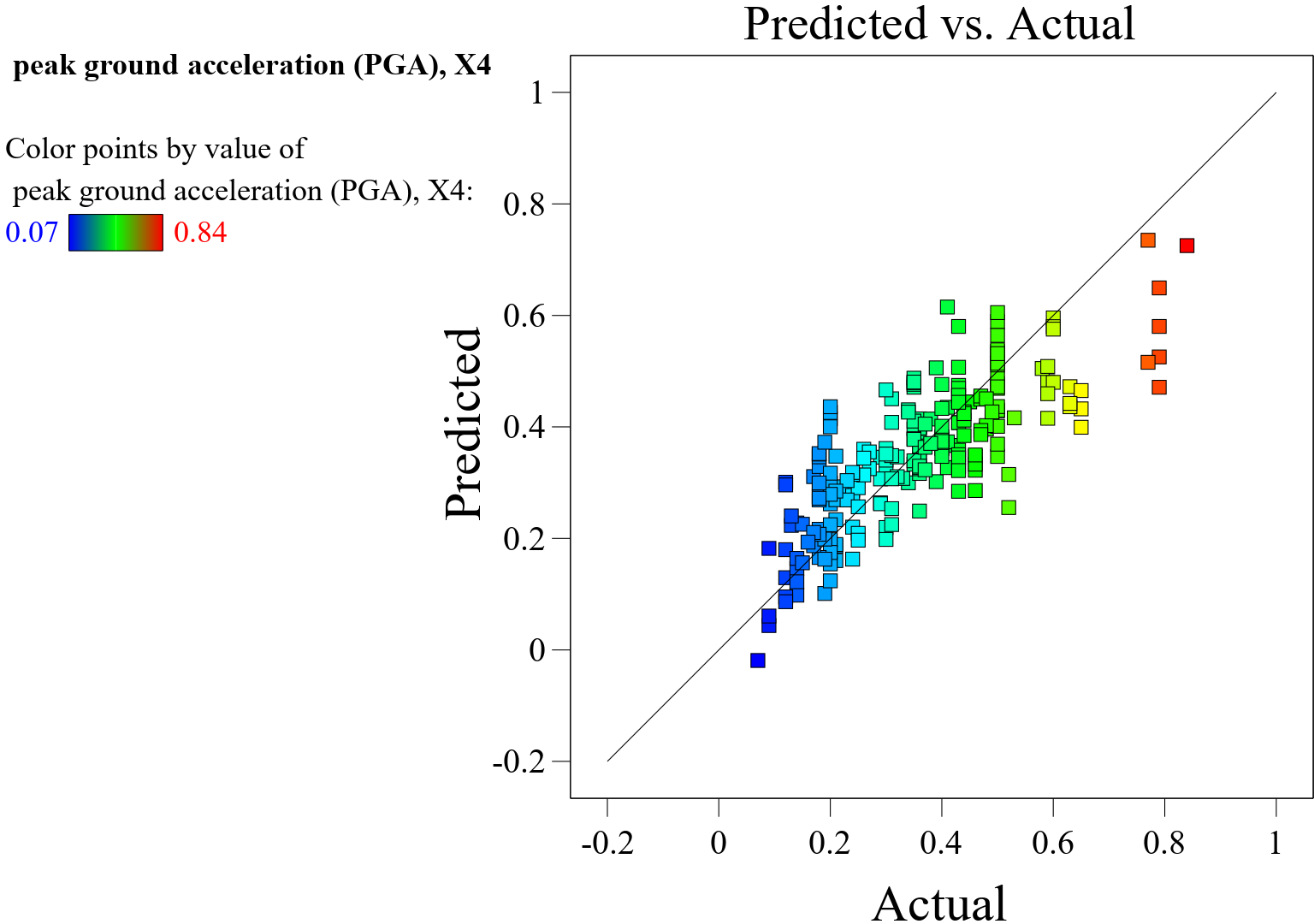
The Figure 8 displays an RSM plot of predicted versus actual Peak Ground Acceleration (PGA) values, where color points represent the magnitude of PGA from 0.07 to 0.84. Key observations and analysis are as follows: The data points are scattered around the diagonal reference line, indicating that the model has a reasonable alignment between predicted and actual PGA values. The closer the points are to this line, the more accurate the predictions. In the lower and middle ranges of PGA (blue to green points), the predictions generally cluster near the diagonal, demonstrating better accuracy. However, for higher PGA values (yellow to red points), the data points show more deviation, indicating potential prediction errors or model limitations in capturing extreme values. Deviations from the reference line, particularly in high-PGA regions, may point to the need for further model improvement or feature enhancement to handle higher magnitude predictions. The color gradient shows a gradual transition across the predicted and actual axes, suggesting a continuous relationship between the predicted and actual PGA values without abrupt shifts. Some points, particularly in the higher PGA range (red points), are far from the diagonal, indicating instances where the model may have overestimated or underestimated PGA. This plot suggests that while the model performs reasonably well for moderate PGA values, further refinement or additional features may be required to enhance its performance for extreme PGA predictions.
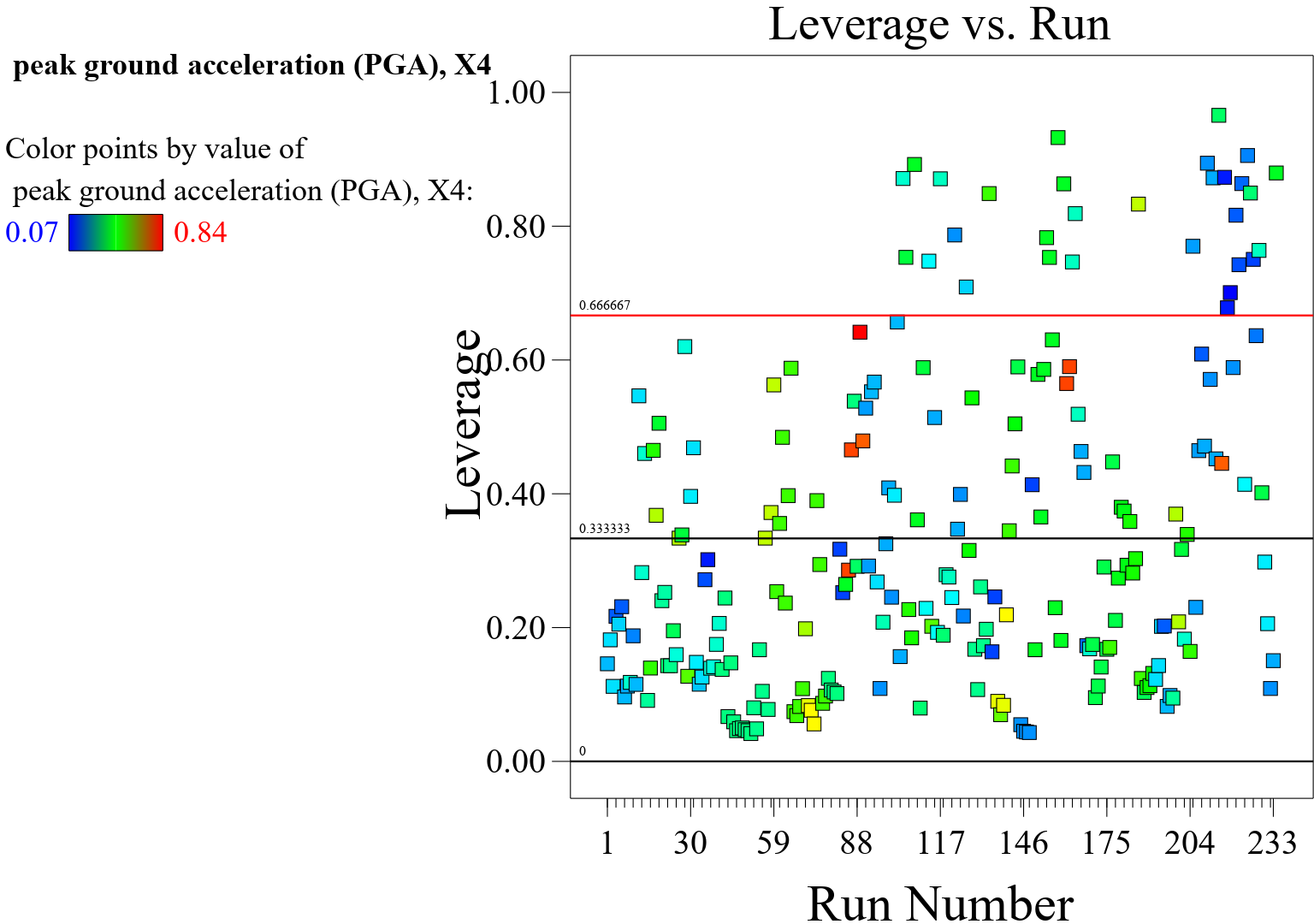

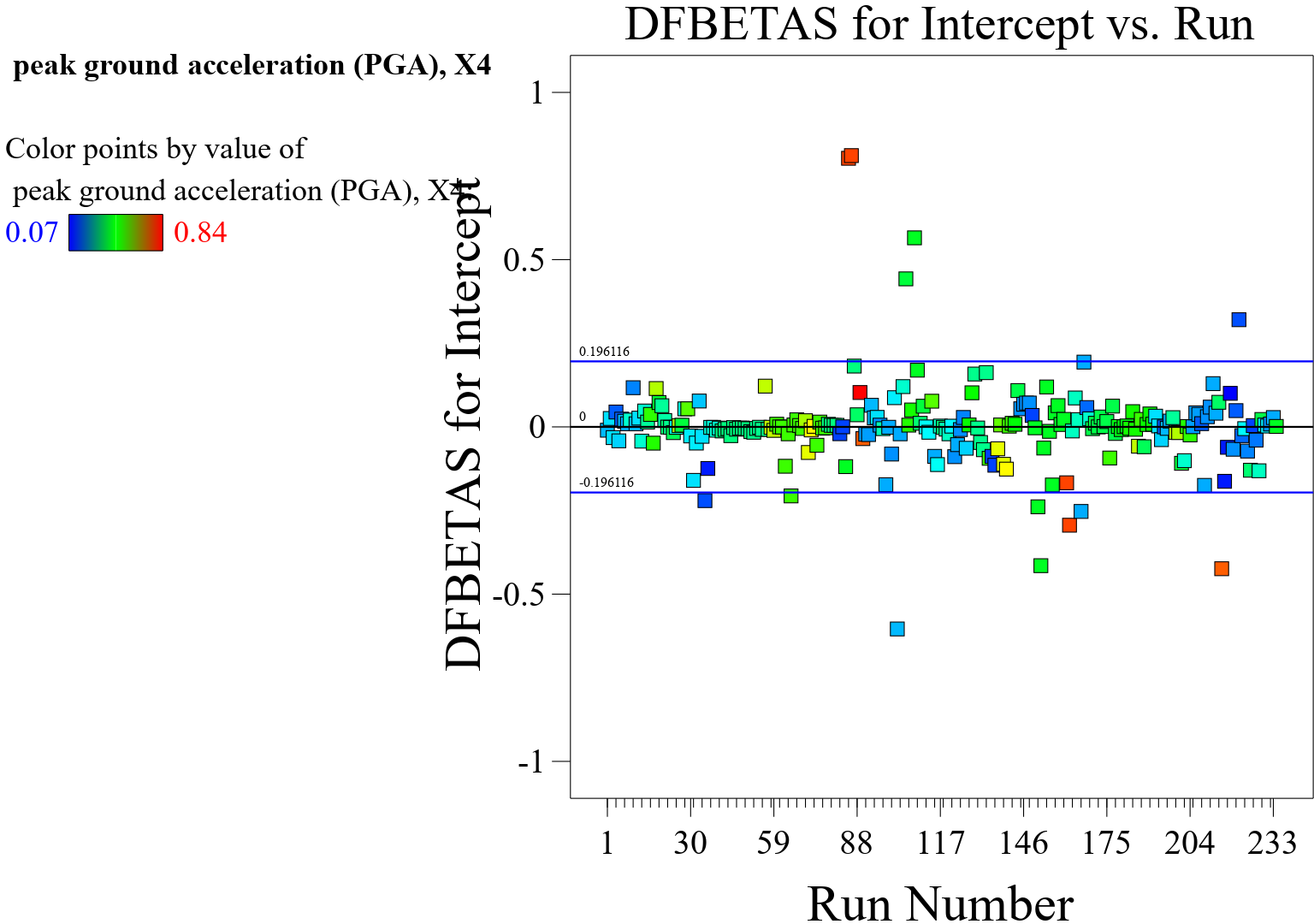
In a response surface model (RSM), a plot of predicted versus actual values illustrated in Figure 8 is a useful diagnostic tool for evaluating the model’s predictive performance and identifying potential discrepancies between the predicted values generated by the model and the actual observed values from the data. In an ideal situation, the predicted versus actual values plot would show a strong linear relationship, with the points falling close to the 45-degree line (). This would indicate that the model’s predictions closely match the actual observed values. If the points on the plot deviate systematically from the 45-degree line, it suggests that the model may have biases or shortcomings in its predictive capabilities. For example, if the model consistently underestimates or overestimates the actual values across a range of predictions, this could indicate a systematic issue. The spread of the points around the 45-degree line can also provide insights into the variability of the model’s predictions. If the spread of points widens or narrows as the actual values increase, it may suggest issues with heteroscedasticity, where the variance of the errors is not consistent across the range of predictions, as shown in Figures 9, 10, 11, 12 and 13. The plot can help identify outliers or influential points that may have a large impact on the model’s predictive performance. Outliers may appear as points that deviate significantly from the expected pattern on the plot. Overall, the plot of predicted versus actual values serves as a valuable diagnostic tool for assessing the accuracy and reliability of the RSM model’s predictions. It helps in identifying potential model misspecification, biases, heteroscedasticity, and influential observations. In summary, the plot of predicted versus actual values in an RSM model provides insights into the model’s predictive performance, highlighting areas where the model’s predictions align well with the actual data and areas where improvements may be necessary.
The RSM research model demonstrates novelty through its ability to comprehensively explore the relationships between multiple independent variables and response variables within complex systems, such as predicting Peak Ground Acceleration (PGA). By employing a structured experimental design combined with regression techniques, it offers a versatile platform for optimizing outcomes and understanding intricate interactions among parameters. A significant aspect of its practical relevance is its potential for real-world problem-solving in geotechnical and seismic applications. The model allows researchers and engineers to develop predictive frameworks capable of improving structural resilience by accurately forecasting seismic behaviors. The capacity of RSM to visualize trends, optimize operating conditions, and provide solutions with minimized experimentation makes it a valuable tool for resource-efficient analysis. Additionally, integrating desirability functions enables multi-objective optimization, allowing stakeholders to balance competing performance criteria such as cost, safety, and sustainability. This versatility makes the RSM model an innovative and indispensable approach to enhancing decision-making processes in infrastructure development and geophysical flow predictions.
In this research work, forecasting earthquake-induced ground movement under seismic activity using the symbolic machine learning technique known as the Response Surface Methodology (RSM) has been studied through data curation, sorting and regression analysis. The learning ability of the symbolic machine learning techniques to propose closed-form equations has been utilized in this research protocol. A global data representative for earthquake-induced ground movements leading to debris flows and other geohazards and geophysical flow events across the world of 234 entries was collected and deployed in the exercise. The earthquake-induced ground movement related parameters that were studied are the earthquake’s moment magnitude (Mw) represented by , epicenter distance (R) denoted as in kilometers, bracketed duration (t) indicated by in seconds, gravel content (G) as in percentage, fines content (F) denoted by in percentage, average particle size (D50) represented by in millimeters, overburden stress-corrected dynamic penetration test blow count (N’120 Blows) indicated by , vertical effective overburden stress (’v) represented by in kilopascals (kPa), depth to the water table (Dw) as in meters, thickness of the impermeable capping layer (Hn) denoted by in meters, and thickness of the unsaturated zone between the groundwater table and capping layer (Dn) as in meters. At the end of the intelligent learning exercise, the following are concluded:
Different from what has been studied in previous research projects, the parameters were rearranged to achieve the focus of this research paper, which is to study the peak ground movement as the model output.
The RSM produced graphical surface configurations which show the behavior of the studied ground movement with respect to the behavior of the input soil parameters.
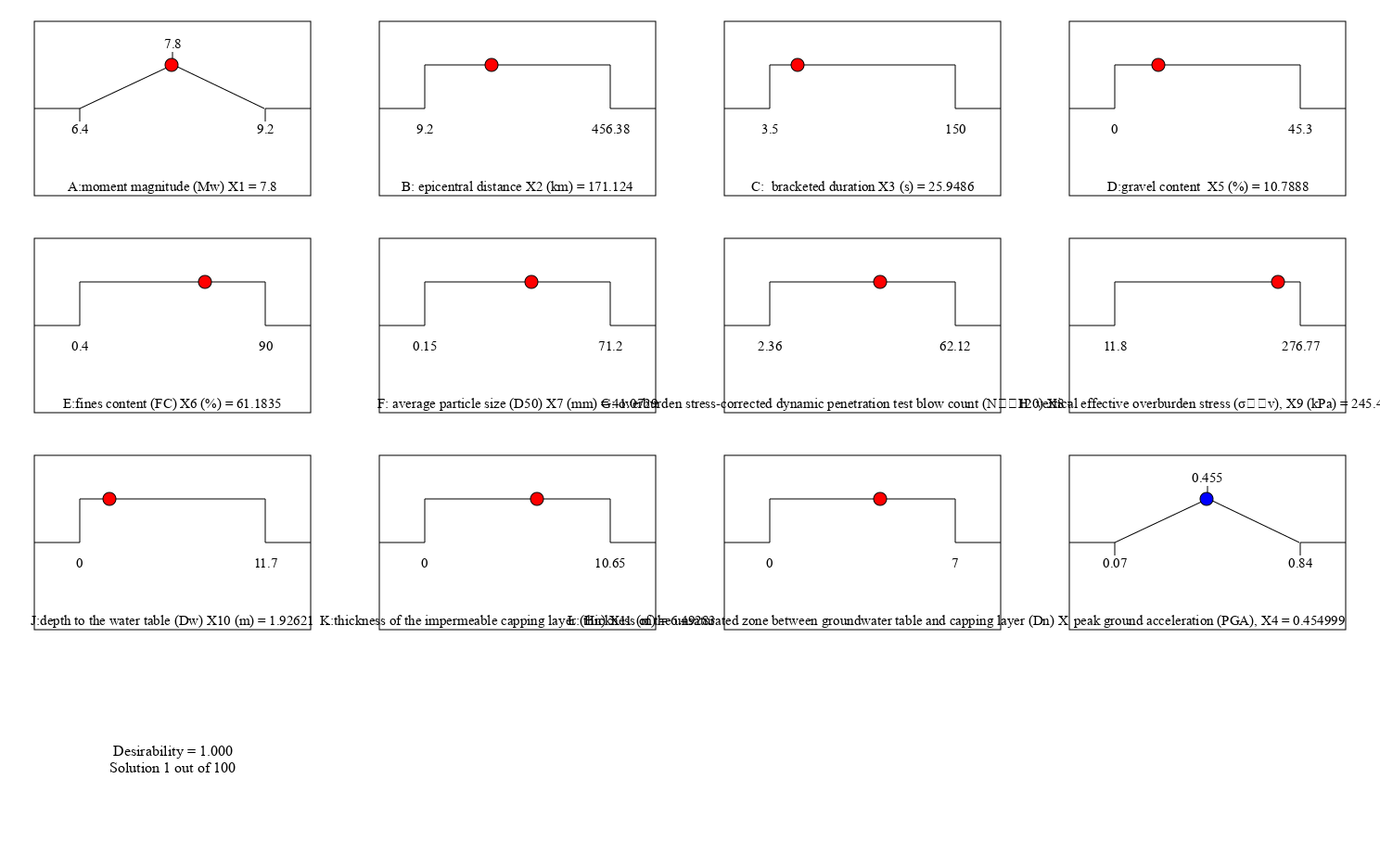
The RSM produced 100 solutions from where the desirability of optimized PGA values was proposed.
Overall, the RSM has proposed a symbolic model with a coefficient of determination of 0.9997 and an adequate precision of 11.1577. The proposed model can design the earthquake-induced ground movement across lands prone to earthquakes with a high degree of accuracy and precision.
 Copyright © 2025 by the Author(s). Published by Institute of Emerging and Computer Engineers. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
Copyright © 2025 by the Author(s). Published by Institute of Emerging and Computer Engineers. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. Sustainable Intelligent Infrastructure
ISSN: request pending (Online) | ISSN: request pending (Print)
Email: [email protected]

Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/iece/